Sheaves On Complex Manifolds . We can introduce a sheaf of c∞ functions on any n dimensional complex manifold, so as to make it into a 2n dimensional c ∞ manifold. Let mbe a complex manifold. Houzel's historical overview of the development of sheaf theory will identify important landmarks for students and will be a pleasure to read for. Here are a few examples: The sheaf of holomorphic functions, the sheaf of c1. Manifolds and varieties via sheaves. This book explains techniques that are essential in almost all branches of modern geometry such as algebraic geometry, complex geometry, or. Manifolds and varieties via sheaves lemma 1.2.7. Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. In rough terms, a manifold is a topological space along with a distinguished collection of functions,.
from blog.twitter.com
Manifolds and varieties via sheaves. Manifolds and varieties via sheaves lemma 1.2.7. In rough terms, a manifold is a topological space along with a distinguished collection of functions,. Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. Houzel's historical overview of the development of sheaf theory will identify important landmarks for students and will be a pleasure to read for. This book explains techniques that are essential in almost all branches of modern geometry such as algebraic geometry, complex geometry, or. We can introduce a sheaf of c∞ functions on any n dimensional complex manifold, so as to make it into a 2n dimensional c ∞ manifold. Here are a few examples: Let mbe a complex manifold. The sheaf of holomorphic functions, the sheaf of c1.
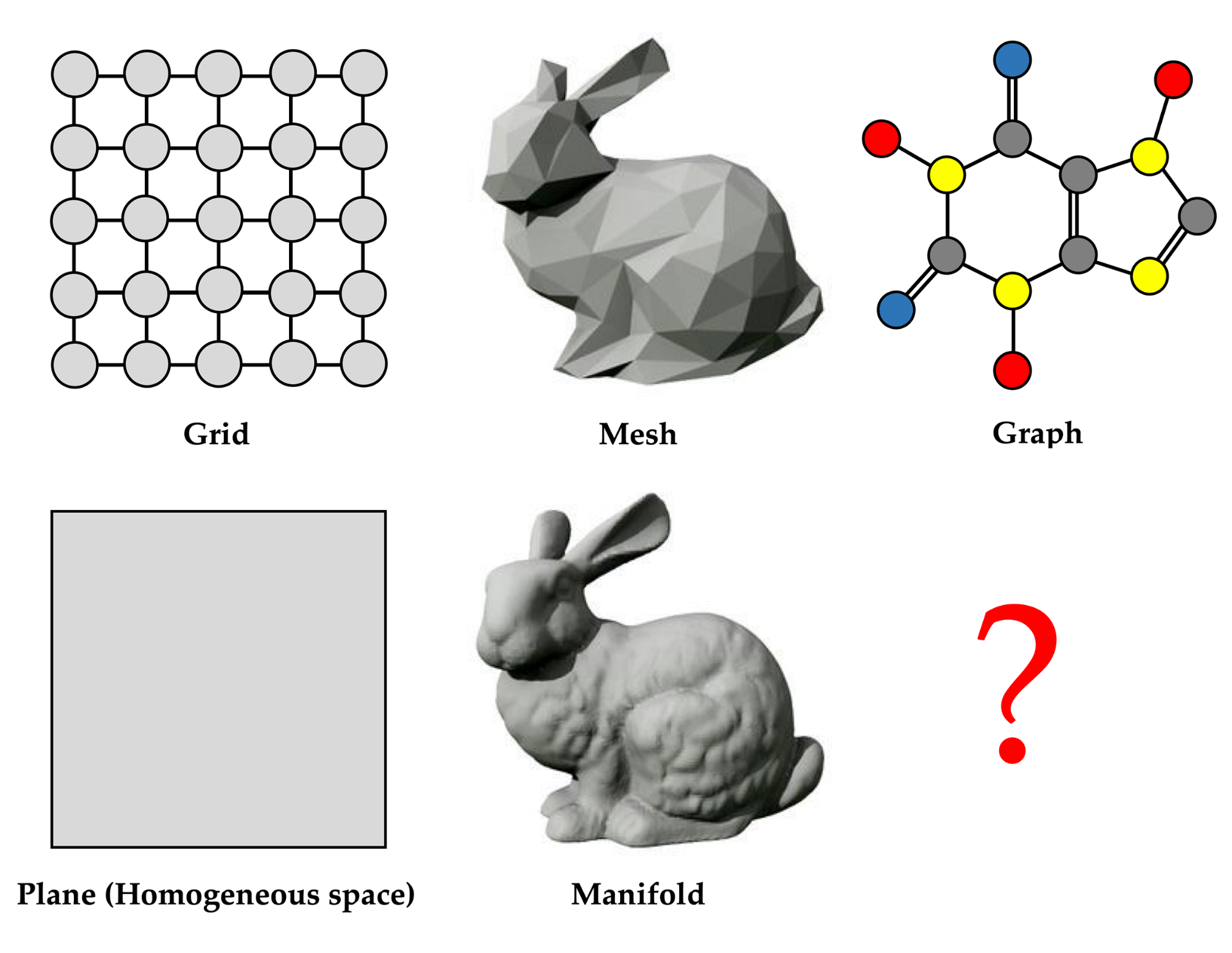
GNNs through the lens of differential geometry and algebraic topology
Sheaves On Complex Manifolds Here are a few examples: Houzel's historical overview of the development of sheaf theory will identify important landmarks for students and will be a pleasure to read for. We can introduce a sheaf of c∞ functions on any n dimensional complex manifold, so as to make it into a 2n dimensional c ∞ manifold. This book explains techniques that are essential in almost all branches of modern geometry such as algebraic geometry, complex geometry, or. Manifolds and varieties via sheaves. Here are a few examples: Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. Let mbe a complex manifold. Manifolds and varieties via sheaves lemma 1.2.7. In rough terms, a manifold is a topological space along with a distinguished collection of functions,. The sheaf of holomorphic functions, the sheaf of c1.
From www.pinterest.com
CalabiYau manifolds are complex manifolds that are generalizations of Sheaves On Complex Manifolds Manifolds and varieties via sheaves lemma 1.2.7. In rough terms, a manifold is a topological space along with a distinguished collection of functions,. Houzel's historical overview of the development of sheaf theory will identify important landmarks for students and will be a pleasure to read for. Let mbe a complex manifold. This book explains techniques that are essential in almost. Sheaves On Complex Manifolds.
From device.report
ESBE GRB300 Manifolds for 2 Circulation Units Instruction Manual Sheaves On Complex Manifolds Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. In rough terms, a manifold is a topological space along with a distinguished collection of functions,. Houzel's historical overview of the development of sheaf theory will identify important landmarks for students and will be a pleasure to read for.. Sheaves On Complex Manifolds.
From sheavescanada.com
Sheaves Canada Sheaves On Complex Manifolds Let mbe a complex manifold. We can introduce a sheaf of c∞ functions on any n dimensional complex manifold, so as to make it into a 2n dimensional c ∞ manifold. Manifolds and varieties via sheaves. Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. Manifolds and varieties. Sheaves On Complex Manifolds.
From www.scribd.com
Sheaves Manifolds PDF Teaching Mathematics Mathematical Analysis Sheaves On Complex Manifolds Manifolds and varieties via sheaves. We can introduce a sheaf of c∞ functions on any n dimensional complex manifold, so as to make it into a 2n dimensional c ∞ manifold. Manifolds and varieties via sheaves lemma 1.2.7. Here are a few examples: This book explains techniques that are essential in almost all branches of modern geometry such as algebraic. Sheaves On Complex Manifolds.
From blog.twitter.com
GNNs through the lens of differential geometry and algebraic topology Sheaves On Complex Manifolds Here are a few examples: Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. Manifolds and varieties via sheaves. We can introduce a sheaf of c∞ functions on any n dimensional complex manifold, so as to make it into a 2n dimensional c ∞ manifold. Manifolds and varieties. Sheaves On Complex Manifolds.
From sheavescanada.com
Sheaves Canada Sheaves On Complex Manifolds In rough terms, a manifold is a topological space along with a distinguished collection of functions,. Manifolds and varieties via sheaves lemma 1.2.7. The sheaf of holomorphic functions, the sheaf of c1. Houzel's historical overview of the development of sheaf theory will identify important landmarks for students and will be a pleasure to read for. We can introduce a sheaf. Sheaves On Complex Manifolds.
From www.youtube.com
What is a Manifold? YouTube Sheaves On Complex Manifolds Manifolds and varieties via sheaves lemma 1.2.7. Here are a few examples: Let mbe a complex manifold. Manifolds and varieties via sheaves. Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. This book explains techniques that are essential in almost all branches of modern geometry such as algebraic. Sheaves On Complex Manifolds.
From www.amazon.com
Vanishing Theorems on Complex Manifolds (Progress in Mathematics) B Sheaves On Complex Manifolds Manifolds and varieties via sheaves. Let mbe a complex manifold. Here are a few examples: In rough terms, a manifold is a topological space along with a distinguished collection of functions,. This book explains techniques that are essential in almost all branches of modern geometry such as algebraic geometry, complex geometry, or. We can introduce a sheaf of c∞ functions. Sheaves On Complex Manifolds.
From www.scribd.com
Complex Manifolds PDF Differentiable Manifold Holomorphic Function Sheaves On Complex Manifolds The sheaf of holomorphic functions, the sheaf of c1. This book explains techniques that are essential in almost all branches of modern geometry such as algebraic geometry, complex geometry, or. Let mbe a complex manifold. Houzel's historical overview of the development of sheaf theory will identify important landmarks for students and will be a pleasure to read for. We can. Sheaves On Complex Manifolds.
From www.perlego.com
[PDF] Introduction to Complex Manifolds, An by eBook Perlego Sheaves On Complex Manifolds Here are a few examples: In rough terms, a manifold is a topological space along with a distinguished collection of functions,. This book explains techniques that are essential in almost all branches of modern geometry such as algebraic geometry, complex geometry, or. We can introduce a sheaf of c∞ functions on any n dimensional complex manifold, so as to make. Sheaves On Complex Manifolds.
From hydair.co.uk
Cetop 3 Manifold Blocks 300 Bar (Steel) Hydair Sheaves On Complex Manifolds Here are a few examples: Manifolds and varieties via sheaves. Manifolds and varieties via sheaves lemma 1.2.7. Let mbe a complex manifold. This book explains techniques that are essential in almost all branches of modern geometry such as algebraic geometry, complex geometry, or. Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric. Sheaves On Complex Manifolds.
From hcs-control-systems.com
Sheaves HCS Sheaves HCS Sheaves On Complex Manifolds Here are a few examples: Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. In rough terms, a manifold is a topological space along with a distinguished collection of functions,. Manifolds and varieties via sheaves lemma 1.2.7. The sheaf of holomorphic functions, the sheaf of c1. This book. Sheaves On Complex Manifolds.
From aspac.com.sg
Enerpac 14″ Long Manifold with 7 Female Ports ASPAC Industrial Tools Sheaves On Complex Manifolds In rough terms, a manifold is a topological space along with a distinguished collection of functions,. Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. Houzel's historical overview of the development of sheaf theory will identify important landmarks for students and will be a pleasure to read for.. Sheaves On Complex Manifolds.
From ind-sup.co.uk
MANIFOLD G1/8 6 POSITION Industrial Supply Specialists Sheaves On Complex Manifolds Here are a few examples: This book explains techniques that are essential in almost all branches of modern geometry such as algebraic geometry, complex geometry, or. We can introduce a sheaf of c∞ functions on any n dimensional complex manifold, so as to make it into a 2n dimensional c ∞ manifold. Let mbe a complex manifold. Sheaf theory is. Sheaves On Complex Manifolds.
From math.stackexchange.com
sheaf theory A question regarding the homotopy method in "Sheaves on Sheaves On Complex Manifolds Manifolds and varieties via sheaves lemma 1.2.7. Manifolds and varieties via sheaves. This book explains techniques that are essential in almost all branches of modern geometry such as algebraic geometry, complex geometry, or. Houzel's historical overview of the development of sheaf theory will identify important landmarks for students and will be a pleasure to read for. We can introduce a. Sheaves On Complex Manifolds.
From ps.is.mpg.de
Learning on Manifolds Perceiving Systems Max Planck Institute for Sheaves On Complex Manifolds Here are a few examples: Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. The sheaf of holomorphic functions, the sheaf of c1. This book explains techniques that are essential in almost all branches of modern geometry such as algebraic geometry, complex geometry, or. We can introduce a. Sheaves On Complex Manifolds.
From www.degruyter.com
On Uniformization of Complex Manifolds Sheaves On Complex Manifolds Sheaf theory is a powerful tool, which allows us to unveil the links between topological and geometric properties of complex manifolds. Houzel's historical overview of the development of sheaf theory will identify important landmarks for students and will be a pleasure to read for. Manifolds and varieties via sheaves. Let mbe a complex manifold. The sheaf of holomorphic functions, the. Sheaves On Complex Manifolds.
From www.physicsforums.com
String theory, CalabiYau manifolds, complex dimensions Sheaves On Complex Manifolds Manifolds and varieties via sheaves lemma 1.2.7. The sheaf of holomorphic functions, the sheaf of c1. In rough terms, a manifold is a topological space along with a distinguished collection of functions,. We can introduce a sheaf of c∞ functions on any n dimensional complex manifold, so as to make it into a 2n dimensional c ∞ manifold. Let mbe. Sheaves On Complex Manifolds.